티스토리 뷰
부스트캠프
[논문 읽기] Fine-Tuning Pre trained Language Models:Weight Initializations, Data Orders, and Early Stopping
eunhhyy 2023. 12. 25. 23:47Abstract
- 동일한 하이퍼파라미터 값으로도 시드를 랜덤으로 설정하면 다른 결과를 낼 수 있음.(성능의 차이가 생길 수 있음)
- 각 데이터셋마다 BERT의 시드만을 변경하며 실험을 진행함.
- 이전 결과와 비교하여 상당한 성능 향상을 확인하였고, 최상의 모델 성능이 실험 횟수에 따라 어떻게 변하는지 정량화해봄.
- 시드 선택에 영향을 받는 두 가지 요소: 가중치 초기화와 훈련 데이터 순서가 모두 검증 세트 성능의 분산에 비례하여 기여한다는 것을 발견함.
- 일부 가중치 초기화는 잘 수행되지만 작은 데이터셋에서는 대부분 학습 중간에 발산하는 것을 관찰하였고, 실험을 조기에 중단하는 방법을 제안함.
1. Introduction

- MRPC ( Microsoft Research Paraphrase Corpus) : 문장 쌍 데이터, 의미가 같은지 아닌지
- RTE ( Recognizing Textual Entailment ) : 두 개의 문장 쌍, 첫 번째 문장(전제)이 두 번째 문장(가설)을 함의하는지를 예측
- CoLA ( Corpus of Linguistic Acceptability ) : 영어 문장을 포함하며, 문법적으로 올바른지 아닌지
- SST (Staford Sentiment Treebank ) : 영화 리뷰에서 긍정적인 또는 부정적인 감정을 나타내는 문장
- 학습 데이터 순서와 가중치 초기화만(모델 파라미터의 0.0006%)을 변경하여 실험을 진행하였고 상당한 차이를 발견함.
- 실험에서 시드만 변경하였음에도 불구하고, 동일한 모델에 대한 이전 발표와 비교하여 상당한 개선이 있음을 확인함.
- MRPC에서는 BERT가 XLNet, RoBERTa 및 ALBERT와 같은 더 최근의 모델보다 더 나은 성능을 보임.
- RTE, CoLA에서는 동일 모델에 대해 7%의 성능 개선을 확인함.
- 이러한 결과는 벤치마크에서 보고된 성능만을 고려하는 모델 비교가 오도될 수 있음을 보여줌.
- fine-tuning에 대한 높은 분산을 이해하기 위해, 가중치 초기화와 훈련 데이터 순서의 영향 요인을 분리하여 알아봄.
- 가중치 초기화와 훈련 데이터 순서를 제어하는 무작위 시드를 설정하여 실험을 수행하였고, 실행 간 분산에 대한 기여를 정량화함.
- 가중치 초기화와 데이터 순서 모두에서 특정 시드가 특정 데이터셋에서 일관되게 더 나은 성능을 보인다는 증거를 제시함.
- 일부 가중치 초기화는 모든 연구된 작업에서 잘 수행됨.
- 모델을 훈련 중 자주 평가함. 성능이 낮은 모델과 성능이 좋은 모델을 훈련 초기에 구별할 수 있음을 관찰
- 필요한 계산 자원을 줄이는 데 효과적인 방법인 간단한 early stopping알고리즘을 보여줌 (5절)
2. Methodology
2.1 Data
- MRPC (Microsoft Research Paraphrase Corpus)
문장 쌍 데이터셋으로, 거의 의미적으로 동등한 문장 쌍과 그렇지 않은 문장 쌍으로 레이블링 되어 있음.
이 데이터셋은 F1과 정확도의 평균을 사용하여 평가됨. - RTE ( Recognizing Textual Entailment )
두 개의 문장 쌍으로 이루어져 있고, 첫 번째 문장(전제)이 두 번째 문장(가설)을 함의하는지 예측하는 것이 과제 - CoLA ( Corpus of Linguistic Acceptability )
영어 문장 데이터셋으로, 문법적으로 올바른 문장과 그렇지 않은 문장으로 레이블링 되어있음.
이 데이터셋은 문장 수준에서의 언어적 수용 가능성을 평가하기 위해 만들어졌고, Matthews 상관 계수를 사용하여 모델을 평가하고, 이는 -1~1 사이의 값을 가지며 무작위 추측의 경우는 0. - SST (Stanford Sentimen Treebank )
영화 리뷰에서 수집된 긍정적 또는 부정적 감성을 나타내는 문장으로 주석이 달려있음.
이 데이터셋은 감성 분석을 위해 만들어졌으며, 이 연구에서는 이진 버전의 주석을 사용
2.2. Fine-tuning
- BERT를 3 epoch동안 fine-tuning진행.
- 전체 모델을 fine-tuning하며, 대부분의 매개변수는 사전 학습된 가중치를 가지고 있으며, 마지막 레이어(2048개의 매개변수)는 무작위로 초기화
- 최종 분류 레이어의 가중치는 BERT, RoBERTa, ALBERT와 같은 사전 학습된 transformer를 fine-tuning할 때 사용되는 표준적인 방법을 사용하여 초기화됨 (평균이 0이고 표준 편차가 0.02인 정규 분포에서 샘플링)
- batch size = 16, lr = 0.00002, dropout = 0.1로 설정
- 각 실험은 N^2번 반복, 가중치 초기화에 대한 N개의 서로 다른 랜덤 시드와 데이터 순서에 대한 N개의 랜덤 시드의 가능한 모든 조합으로 수행. MRPC, RTE, CoLA 데이터셋에 대해 각각 625번 실험을 진행하였고 (N=25), SST의 경우 225번 실험 진행 (N=15)
3. The large impact of random seeds
- 시드만 변경한 실험은 성능의 상당한 변동을 보여줌. 특히 작은 데이터셋에서 두드러지며, 여러 번의 실험에서 찾은 최상의 모델의 검증 성능은 단일 시도의 예상 성능보다 상당히 높음. (실험 횟수가 기대 검증 성능에 미치는 영향을 탐구함)
3.1. Expected validation performance
- 포준 머신 러닝 실험 설정은 연구자가 x개의 모델을 훈련하고, 각각을 검증 데이터로 평가한 다음, 검증 성능이 가장 우수한 모델을 선택하여 테스트 데이터로 평가함.

- 실험 횟수가 증가함에 따른 기대 검증 성능을 나타낸 그래프로 표준 편차를 그림자로 처리함
- 파란색 : 모델이 훈련 중에 검증 세트에서 자주 평가됨.
- 주황색 : 각 epoch 끝에 모델이 평가됨
- 초록색 : 훈련의 끝에만 모델이 평가됨
- 실행당 평가 횟수가 증가함에 따라 더 높은 기대 성능과 더 작은 분산이 나타남.
- 모델을 검증 데이터에서 더 자주 평가할수록 더 높은 기대 검증 값이 나타남.
- 작은 데이터셋인 MRPC, RTE, CoLA의 경우 기대 검증 성능에 상당한 분산이 나타나고, 이는 각각의 실행이 서로 다른 성능을 보일 수 있다는 것을 의미함. 즉, 동일한 모델 및 하이퍼파라미터를 사용하더라도, 각 실행 간에 성능 차이가 크게 발생할 수 있음을 의미함.
4. Weight initialization and data order

실행 간 검증 성능의 예상(평균) 표준 편차. 주어진 WI, DO 랜덤 시드의 예상 표준 편차는 크기가 비슷하고, 전체 표준 편차보다 약간 작음.
- WI, DO 시드 집합의 모든 조합으로 실험을 진행함.
- 데이터 순서는 훈련 데이터의 순열 집합에서 하나의 샘플로 볼 수 있음.
- 가중치 초기화도 우리가 그들을 뽑는 정규 분포의 특정한 샘플 집합으로 볼 수 있다.
- 데이터 순서는 훈련 데이터의 순열 집합에서 하나의 샘플로 볼 수 있음. 훈련 데이터의 순서를 의미하고 데이터를 섞을 때 어떤 순서로 섞을지를 말하는 것.
- 가중치 초기화는 모델의 가중치를 무작위로 초기화하는 것을 의미하고, 각각의 가중치를 뽑는 것을 정규 분포에서 샘플링한 것으로 생각할 수 있음.

- 실험에서 다양한 초기화 방법과 데이터 순서를 사용하여 모델을 훈련시켰을 때, 각각의 조합이 어떤 성능을 보이는지 보여줌.
- 각 색칠된 셀은 단일 실험에 대한 검증 성능을 나타냄.
- 그림에서 각 행은 단일 가중치 초기화를 나타내고, 각 열은 단일 데이터 순서를 나타냄.
- 평균에 따라 정렬하여 가장 위의 행은 평균 성능이 가장 높은 WI를 가진 실험을 포함하고, 가장 오른쪽 열은 평균 성능이 가장 높은 DO를 가진 실험을 포함함.
- MRPC, RTE, CoLA의 경우, 훈련된 모델 중 일부가 발산하여, 가장 빈번한 레이블을 예측하는 것과 유사한 성능을 보임.
- 이는 Figure1에서 세 데이터셋에 대한 예상 검증 곡선에서 발견된 큰 분산을 부분적으로 설명
4.1. Decoupling
- Decoupling은 두 가지 이상의 변수 또는 요소를 분리하는 것을 의미함. 이 논문에서는 무작위서을 제어하는 두 가지 요소인 가중치 초기화와 데이터 순서를 분리하여 각각의 요소에 따른 성능 분포를 분리하는 것을 말함. 이를 통해 각 요소가 성능에 미치는 영향을 개별적으로 파악할 수 있음.
- 각각의 요소에 대해 다양한 시드를 사용하여 실험을 수행하고, 해당 시드에서 수행된 모든 시행에서의 검증 성능의 표준 편차를 계산
- 이를 통해 각 요소가 성능에 미치는 영향을 개별적으로 파악할 수 있음.
- 가중치 초기화와 데이터 순서는 성능 분산에 비슷한 영향을 미치며, 각각의 요소에서의 예상 표준 편차는 특정 작업 내에서 전체 표준 편차보다 약간 작음.
- 표준 편차는 평균값으로부터 얼마나 떨어져 있는지를 나타내는 측정값
- 표준 편차가 작을수록 데이터가 평균 주변에 모여 있고, 표준 편차가 클수록 데이터가 분산되어 있는 것을 의미함.
- 각 시드에서의 검증 성능이 얼마나 일관되게 나타나는지를 나타내는 지표로 사용
4.2. Some random seeds are better than others

- WI, DO 시드가 다른 시드보다 더 나은지를 알아보기 위해 가장 좋은 평균 성능과 가장 좋지 않은 평균 성능을 보이는 무작위 시드를 나타낸 그래프로 Best와 Worst는 다른 행동을 보임.
- Worst 시드는 낮은 성능 범위에서 상당히 높은 밀도를 가지고 있음
- MRPC, RTE, CoLA와 SST에서는 다른 모습을 보이는데 데이터의 크기와 관련이 있을 것이라고 말함.
- SST데이터는 더 큰 데이터셋으로 순서를 지정할 데이터가 더 많고 초기화에서 멀어지기 위한 가중치 업데이트가 더 많이 있을 것이라고 예상

- ANOVA(분산 분석)를 사용하여 통계적 유의성을 검정하여, 가장 좋은 DO와 가장 나쁜 DO, 그리고 가장 좋은 WI와 가장 나쁜 WI의 성능이 서로 다른 분포를 가지는지 조사함.
- 모든 데이터셋에 대해 가장 좋은 DO와 가장 나쁜 DO, 그리고 가장 좋은 WI와 가장 나쁜 WI의 성능은 유의하게 다른다는 것을 발견
- ANOVA p값은 가장 좋은 WI와 가장 나쁜 WI, 그리고 가장 좋은 DO와 가장 나쁜 DO의 성능이 동일한 평균을 가진 분포를 가지는 귀무가설을 기각할 증거가 있다는 것을 나타냄
- p < 0.05인 경우에는 해당 성능들이 통계적으로 유의하게 다른다는 것을 의미
- 이 표는 가장 좋은 가중치 초기화와 가장 나쁜 가중치 초기화, 그리고 가장 좋은 데이터 순서와 가장 나쁜 데이터 순서의 성능이 서로 다르다는 것을 보여주고 있음.
- ANOVA는 세 개 이상의 그룹 간 평균의 차이를 비교하는 통계적 방법으로 그룹 간의 차이가 통계적으로 유의한 지를 판단하는 데 사용
- ANOVA의 가정 1) 표본의 독립성 : 각 그룹의 표본은 서로 독립적이어야 함. 2) 등분산성 : 각 그룹의 모집단 분산이 거의 동일해야 함.
3) 정규 분포 : 각 그룹의 데이터가 정규 분포를 따라야 함. - ANOVA는 F-통계량을 사용하여 그룹 간의 평균 차이가 우연에 의한 것인지를 판단
- F-통계량은 그룹 간의 변동과 그룹 내의 변동의 비율을 나타내며, 이 비율이 충분히 크면 그룹 간의 평균 차이가 우연에 의한 것이 아니라고 판단
- F-통계량이 크면서 p-value가 작을수록 그룹 간의 평균 차이가 통계적으로 유의하다고 볼 수 있음.
- 만약 그룹 간의 차이가 통계적으로 유의하다면, ANOVA는 적어도 한 그룹이 다른 그룹과는 다른 평균을 가지고 있다는 결론을 내림
- ANOVA는 그룹 간의 크기가 동일하고, 데이터가 정규 분포를 따르지 않더라도 상대적으로 강건한 특성을 가지고 있지만 독립성과 등분산성 가정은 중요하며 이러한 가정이 위반될 경우 ANOVA의 결과를 신뢰할 수 없을 수 있음
- DO와 WI는 샘플이므로 독립적임. ANOVA는 그룹의 크기가 동일하면 그룹 간 분산이 약간 다르더라도 일반적으로 강건함
4.3. Globally good initializations
- 시드는 여러 다른 데이터셋에서도 좋은 성능을 보일 수 있다.
5. Early Stopping
- 무작위로 시드를 설정했을 때 분산이 큼 (모델의 성능이 시드에 따라 크게 흔들릴 수 있음)
- 훈련 초기에 가장 유망하지 않은 실험을 조기에 중단하는 알고리즘을 사용하여 더 나은 성능을 달성할 수 있다는 것을 보여줌.
Early discovery of failed experiments
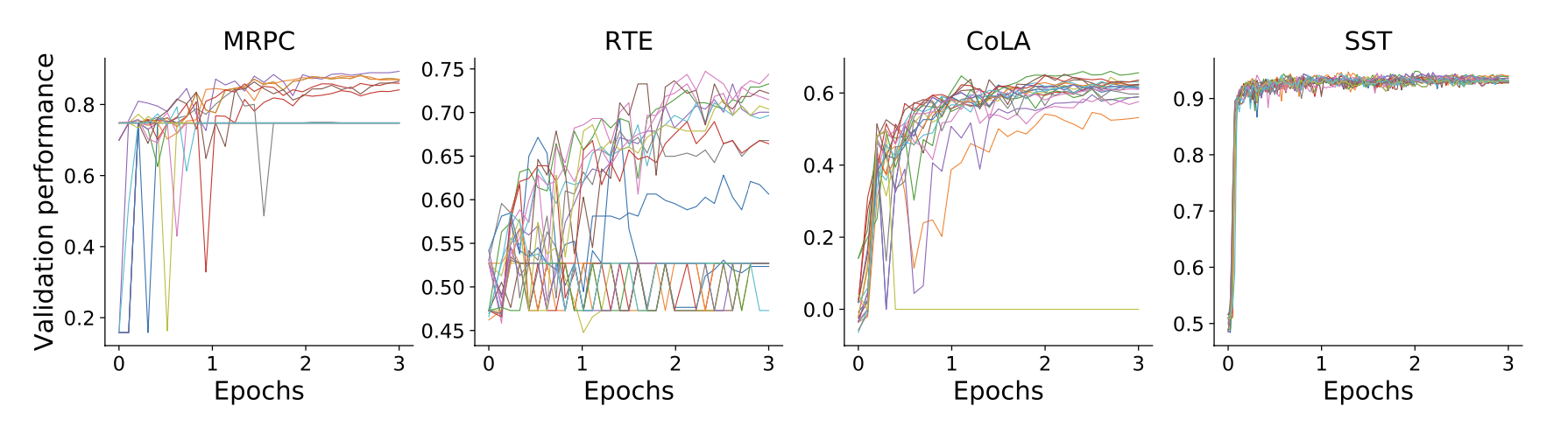
- 훈련 중 다른 시점에서 20개의 무작위 모델의 성능 값을 보여주는 그래프로 훈련 초기에 성능 차이가 빠르게 드러날 수 있다는 것을 보여준다.
- 성능이 낮은 모델을 끝까지 훈련하는 것은 낭비.
- 예를 들어, CoLA에서 첫 번째 에포크의 중간에 훈련을 마친 후, 발산한 모델을 중간할 수 있음.
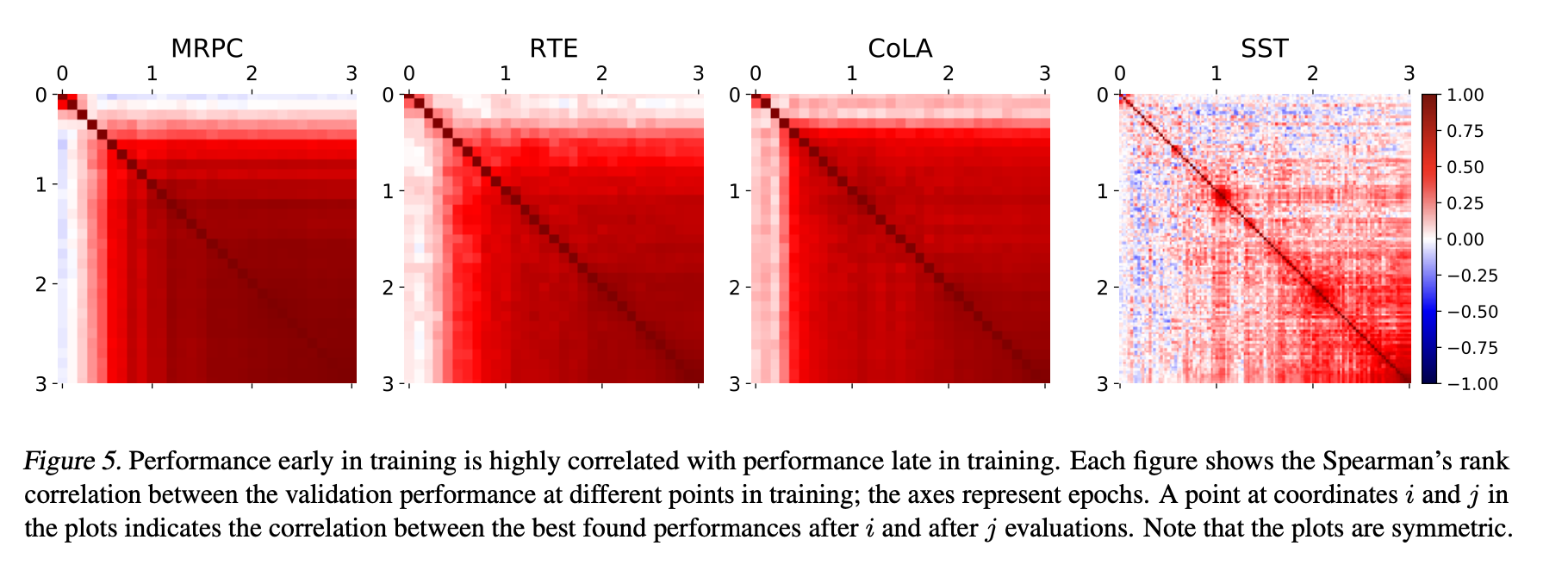
- 이 그림에서의 하나의 점은 i와 j반복에서의 성능 간 스피어만 순위 상관관계를 나타냄
- 높은 순위 상관관계는 두 평가 지점 사이의 모델 순위가 유사하다는 것을 나타내며, 성능이 가장 나쁜 모델을 조기에 중단할 수 있다는 것을 시사함.
- MRPC, RTE 및 CoLA에서는 훈련 초기 모델의 성능과 최종 성능 간에 높은 상관관계가 있음
- 더 큰 SST 데이터셋에서는 2 에포크 훈련 후 성능과 최종 성능 간에 높은 상관관계를 볼 수 있음.
Early Stopping
- 좋은 성능을 가지는 시드를 선택하기 위해 early stopping 알고리즘을 적용
- t : 전체 실험의 수 또는 모델의 수. 이는 전체 실험 중에서 얼마나 많은 모델을 훈련시킬 것인지를 결정
- f : 훈련 중간에 평가를 수행할 때 전체 훈련 단계 중 어느 정도까지 진행한 후에 평가를 수행할지를 나타냄. 이는 각 실험의 일부를 훈련한 후에 얼마나 많은 모델을 평가할 것인지를 결정
- p : 가장 유망한 모델의 수를 나타냄. 훈련 중간에 평가를 마친 후 가장 좋은 성능을 보인 모델 중에서 몇 개의 모델을 선택하여 추가적인 훈련을 진행할 것인지를 결정
- 이 알고리즘은 모델을 완전히 훈련하는데 필요한 단계 수인 s를 곱한 (tf + p(1-f))s 단계를 취함.
start many, stop early, continue some

- 이 알고리즘의 매개변수 t, f, p는 직접 할당하여 계산도 가능하지만,
매개변수 t, f, p를 어떻게 할당하느냐에 따라서 성능이 크게 달라질 수 있기 때문에 이를 평가하기 위해 50,000번의 샘플링을 통해 알고리즘을 시뮬레이션해봄. - 이를 통해 각 매개변수 할당 방법의 성능을 추정하고, 이를 기반으로 최적의 매개변수 할당 방법을 찾을 수 있음.
- 총 훈련 에포크가 3에서 90 사이이거나 초기에 1에서 30개의 여러 개의 모델을 동시에 훈련시켜 해당하는 예산에 대한 최상의 매개변수 할당 방법을 찾음
- 초기 훈련 모델 수는 완전히 훈련된 모델 수보다 훨씬 많아야 하고, 완전히 훈련할 시도 수는 x/2 정도여야 함.
- 4개의 데이터셋 중 3개에서는 훈련 초기에 가장 유망하지 않은 시도를 중단하는 것이 최상의 결과를 가져왔고, 4번째 데이터 셋에서도 이는 강력한 전략이었음.
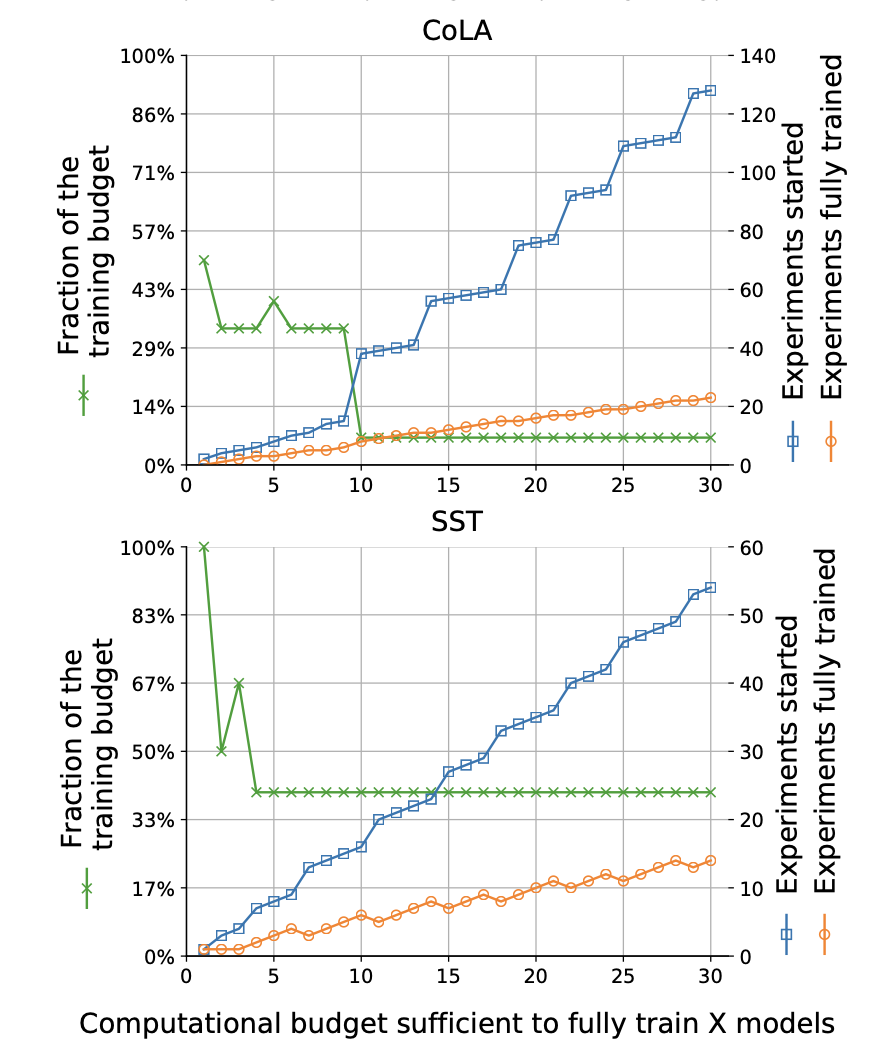
- 그림 6. 각 데이터 세트에서 가장 잘 관찰된 매개변수로 x 모델을 완전히 학습시킬 수 있을 정도로 큰 예산(각각 3개의 에포크에 대해 훈련됨)의 경우, 이 그림은 조기 중지를 위한 최적의 매개변수를 보여줌.
- 예를 들어, MRPC 데이터셋에서 20개의 시도를 할 수 있을 정도로 큰 예산을 가진 경우, 가장 잘 관찰된 성능은 41개의 시도(파란색)를 시작한 다음 30%의 교육(녹색) 후 11개의 가장 유망한 시도(주황색)만 계속함으로써 나타남.
Early Stopping works

- 알고리즘을 조기 중단 없이( f=1, t=p) 여러 실험을 모두 훈련하는 기준선과 동일한 계산량을 사용하여 비교
- t개의 모델을 완전히 훈련하는데 필요한 계산 예산에 해당하는 경우, 해당 계산 예산에 대한 최상의 조기 중단 설정을 사용하여 상대적 오류 감소를 측정
- 왼쪽 그림은 computational budget이 변할 때 각 데이터셋의 상대적 오류 감소를 보여주며, 작은 작업에서는 합리적으로 일관된 개선이 관찰됨.
6. Related Work
- 하이퍼파라미터 최적화에 대한 대부분의 연구는 학습률, 모델의 레이어, 정규화 같은 중요한 하이퍼파라미터를 조정
- 여기서는 하이퍼파라미터로 캐스팅할 수 있는 두 가지 종종 간과되는 선택지만을 조사하고 최적화할 여지가 있다는 것을 발견
- 초기화 분포에 대한 연구는 Xavier 초기화 및 kaiming 초기화와 같은 가중치 초기화 방법에 대해 다루며, 이러한 초기화 방법은 역전파를 통해 그래디언트 크기를 보존하기 위해 분산을 조정하여 가중치를 초기화
- 불확실성과 같은 기준을 사용하여 데이터 순서를 선택하는 방법에 대해 다루며, 다양성을 갖는 미니배치에서 훈련하는 것이 효율적일 수 있다.
- 이 논문에서는 같은 하이퍼파라미터 값을 사용하더라도 서로 다른 랜덤 시드로 인해 결과가 크게 달라질 수 있는 현상을 보여주고 있음
- 모델 실험할 때 가능한 모든 하이퍼파라미터 조합에 대해 여러 번 실험하고, 랜덤 시드를 변경하여 실험을 반복하는 것을 추천
- 이를 통해 모델의 성능을 더욱 정확하게 평가할 수 있고, 최적의 하이퍼파라미터와 초기화 가중치를 찾을 수 있음.
7. conclusion
- 초기화 가중치와 훈련 데이터 순서가 모델 성능 변동에 상당한 영향을 미침을 밝힘
- 일부 데이터 순서와 초기화 가중치가 여러 작업에서 잘 수행됨을 발견
- 여러 번 실험을 수행하는 데 필요한 계산 비용을 줄이기 위해 간단한 조기 중단 방법을 제안
'부스트캠프' 카테고리의 다른 글
| LLaMA-VID: An Image is Worth 2 Tokens in Large Language Models (3) | 2024.01.21 |
|---|---|
| Do PLMs Know and Understand Ontological Knowledge? (0) | 2024.01.06 |
| [논문 읽기] RoBERTa: A Robustly Optimized BERT Pretraining Approach (0) | 2023.12.18 |
| [Boostcamp] 6주차 회고 (0) | 2023.12.15 |
| [Boostcamp] 5주차 회고 (2) | 2023.12.08 |
